Category Archives: research

A New Distribution

By | | , , ,
3 Comments

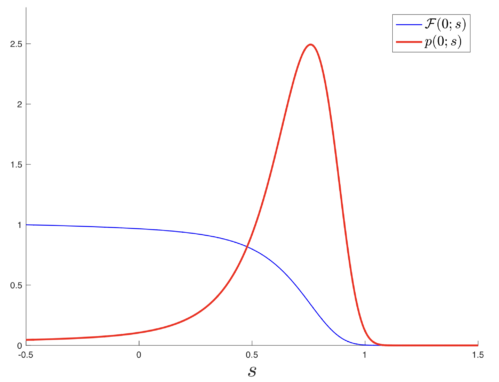Probability distributionThe red curve in this figure is the probability distribution of the ground state energy [latex]E=s[/latex] of the microstate spectra of quantum completions of JT gravity. Put differently (the way Wigner might have) if you ask what are all the discrete spectra that are compatible with the leading semi-classical result for quantizing JT gravity (the famous Schwarzian result for the density of states: [latex]\rho(E)=e^{S_0}(4\pi^2)^{-1}\sinh(2\pi\sqrt{E})[/latex]), this curve gives the shape of the distribution of ground states. (The blue curve is simply the associated CDF.) I first uncovered this distribution in a paper last year, with further insights and generalizations in a paper earlier this year, along with the distributions for higher energy levels that follow from it. But the exciting new result of my paper from a few weeks ago is that I have now shown that it is a solution of an ordinary differential equation (or a family of them). This allows for some powerful universal things to be said analytically about the properties of the distribution!

This is fully analogous to what happened for the well-known Tracy-Widom distribution for the largest (or smallest) energy of Gaussian random hermitian matrices. While many workers (such as Forrester) had uncovered important aspects of the distribution, and while it was known that it can be expressed as a particular Fredholm determinant, Tracy and Widom broke new ground in 1994 by showing that the distribution was governed by a well known ODE – the Painleve II equation – and in particular can be given in terms of a special solution of it studied earlier by Hastings and McLeod. The result helped forge further connections between properties of random matrix theory and several interesting areas of mathematics and mathematical physics. Furthermore, […] Click to continue reading this post →

Embracing Both Wigner and ‘t Hooft

By | | , , , ,
5 Comments

That Feeling

Several weeks ago, while writing up a nice set of results that extended some work I did last year, I found that I was stuck finding the right wording for how I should nuance a (seemingly minor) matter in the introductory remarks. It was partly because, frankly, I’d got bored of the standard introduction I usually make to papers on this particular subject (matrix models and 2D gravity), because I’ve written quite a few in the last two years (10-Yikes!). But I’d found a new feature that warranted a more careful way of saying the usual things, and I wanted to incorporate that aspect, and also get the Reader interested in why this aspect was interesting and worth unpacking. I played around with better ways of saying it, and still was not entirely happy. I chipped away for a bit more over a few days, and kept coming up with something less than satisfactory. I’d carry on with things in the body of the paper that would be there whatever the introduction said. Then, after coming back to the introduction and trying again, I had to stop and explore the consequences of some of the rephrasing I was doing – to make sense of the new way I was trying to say what I wanted to say.

And then it happened…

You might know that feeling: A sort of pop goes off in your head and a tingle through the whole body, and then everything looks different all of a sudden, because you realize that you’ve found a completely new way of looking at things. A way that fits *so* well and incorporates so many of the facts that it just. feels. inevitable.

That’s what happened. And then I tried to see what it would say about the larger picture of physics this all fits in, looking for a way to make it fit, or to challenge the idea to see if it breaks. Not only did not not break, it just kept making sense, and (almost like the idea itself took charge of the process) immediately offered solutions to the problems I threw at it, and readily gobbled up existing challenges that the community has been facing for a while, and explained certain things that have been a puzzle for a long time.

For the next few days I actually could not write properly at the keyboard any more. My hands were trembling every time as I utterly rebuilt the entire paper and my world view, and I could barely sit still at times.

I know this sounds like a lot, and you should know that I am open to the possibility that it is somehow wrong, but it is too compelling not to share, so that’s what my paper that came out earlier this week is all about. I am not going to repeat the paper here, but will try to highlight some features of it that form a foundation for why this changes a lot about how we think about things in this corner of physics.

Random Stuff

Let me start in the simplest way possible, as I have done in the past, with a model that is well known to many different physics communities. The Gaussian random matrix model. Random matrix models have a very long history in trying to understand complicated systems (going back to Wishart (1928), and then Wigner (1955) – physicists seem to always forget to mention Wishart, and I’m sure I’m forgetting someone else too), and they show up in all kinds for systems. There are a lot of powerful results that have been developed, and you’ve read my writings about them here to do with how they get used for understanding aspects of string theory and quantum gravity in 2D, and also in higher dimensions. The “double scaling limit” is something I’ve talked about a lot here in particular. I won’t repeat all of it here, but invite you to go and look at other posts.
[…] Click to continue reading this post →

Completing a Story

By | | , , , ,
1 Comment

[A rather technical post follows.]

[caption id="attachment_19916" align="aligncenter" width="499"]Sample image from paper. Will be discussed later in the text. This figure will make more sense later in the post. It is here for decoration. Sit tight.[/caption]

For curious physicists following certain developments over the last two years, I’ll put below one or two thoughts about the new paper I posted on the arXiv a few days ago. It is called “Consistency Conditions for Non-Perturbartive Completions of JT Gravity”. (Actually, I was writing a different paper, but a glorious idea popped into my head and took over, so this one emerged and jumped out in front of the other. A nice aspect of this story is that I get to wave back at myself from almost 30 years ago, writing my first paper in Princeton, waving to myself 30 years in the future. See my last post about where I happen to be visiting now.) Anyway here are the thoughts:

Almost exactly two years ago I wrote a paper that explained how to define and construct a non-perturbatively stable completion of JT gravity. It had been defined earlier that year as a perturbative […] Click to continue reading this post →

A Return

By | | , , , , , ,
5 Comments

Well, I’m back.

It has been very quiet on the blog recently because I’ve been largely occupied with the business of moving. Where have I moved to? For the next academic year I’ll be on the faculty at Princeton University (as a Presidential Visiting Scholar) in the Physics department. It’s sort of funny because, as part of the business of moving forward in my research, I’ve been looking back a lot on earlier eras of my work recently (as you know from my last two year’s exciting activity in non-perturbative matrix models), and rediscovering and re-appreciating (and then enhancing and building on) a lot of the things I was doing decades ago… So now it seems that I’m physically following myself back in time too.

Princeton was in a sense my true physical first point of entry into the USA: My first postdoc was here (at the Institute for Advanced Study, nearby), and I really began […] Click to continue reading this post →

Full Circle

By | | , , , ,
Comments Off on Full Circle

snapshot of paper

Yesterday I submitted (with collaborators Felipe Rosso and Andrew Svesko) a new paper to the arXiv that I’m very excited about! It came from one of those lovely moments when a warm flash of realisation splashed through my mind, and several fragments of (seemingly separate things) that had been floating around in my head for some time suddenly all fit together. The fit was so tight and compelling that I had a feeling of certainty that it just “had to be right”. It is a great feeling, when that happens. Of course, the details had to be worked out, and everything checked and properly developed, new tools made and some very nice computations done to unpack the consequences of the idea… and that’s what resulted in this paper! It is a very natural companion to the cluster of papers I wrote last year, particularly the ones in May and June.

What’s the story? It’s all about Jackiw-Teitelboim (JT) gravity, a kind of 2D gravity theory that shows up rather generically as controlling the low temperature physics of a wide class of black holes, including 4D ones in our universe. Understanding the quantum gravity of JT is a very nice step in understanding quantum properties of black holes. This is exciting stuff!

Ok, now I’ll get a bit more technical. Some background on all this (JT gravity, matrix models, etc), can be found in an earlier pair of posts. You might recall that in May last year I put out a paper where I showed how to define, fully non-perturbatively, a class of Jackiw-Teitelbiom (JT) supergravity theories that had been defined in 2019 in a massive paper by Stanford and Witten (SW). In effect, I showed how to build them as a particular combination of an infinite number of special “minimal string” models called type 0A strings. Those in turn are made using a special class of random matrix model based on […] Click to continue reading this post →

Shaping the Future of Scientific Conferences

By | | , , , ,
Comments Off on Shaping the Future of Scientific Conferences

This year’s big annual flagship conference in String theory, Strings 2020, ended two days ago. It was a massive success, and it was held entirely online. There were more than 2000 registered participants from all around the world, with sessions where a large portion of that number were engaged simultaneously! This conference’s attendance more usually ranges at around 300 – 400, as far as I remember, so this was a spectacular change. The success was made possible by -most importantly- the willingness of many people to take part and engage with each other to a degree that was foreign to most participants, combined with smart and tireless effort by the team of organizers in Cape Town, where the conference was originally going to be held physically. There were excellent talks (selected by the programme committee) and many illuminating discussions.

Due to the pandemic, the conference was originally going to be cancelled (or at least postponed to much later in the year), but organizer Jeff Murugan announced at relatively short notice that they were instead going to attempt to do it online on the original dates, and it is wonderful that so many people around the world engaged, instead of just shrinking away into the Covid-19 gloom.

The other major component of the success is what I want to discuss here. It was the use, sometimes in concert, of tools such as Zoom […] Click to continue reading this post →

Spectral, II

By | | , , , ,
3 Comments

plot of spectral density of (2,2) JT SupergravityWhat’s that now? You want more physics teases? Ok. That dotted line is a (known) JT gravity Schwarzian spectral density. That red line? It’s the fully quantum corrected result! To all orders in topology and beyond. See my paper that appeared today on the arXiv.

(For experts: The red line is made up of about 2000 points for each of which I know the energy, and the full wave function for an associated problem. Using those I can compute lots of things, to good accuracy. One example is the full non-perturbative spectral form factor, that I showed last post.)

-cvj Click to continue reading this post →

Black Holes and a Return to 2D Gravity! – Part II

By | | , , , ,
Comments Off on Black Holes and a Return to 2D Gravity! – Part II

(A somewhat more technical post follows.)

Continuing from part I: Well, I set the scene there, and so after that, a number of different ideas come together nicely. Let me list them:

[caption id="attachment_19442" align="alignright" width="250"]illustration of JT gravity background What “nearly” AdS_2 looks like via JT gravity. The boundary wiggles, but has fixed length 1/T.[/caption]
  • Exact solution of the SYK model (or dual JT model) in that low temperature limit I mentioned before gave an answer for the partition function $latex Z(\beta)$, by solving the Schwarzian dynamics for the wiggling boundary that I mentioned earlier. (The interior has a model of gravity on $latex AdS_2$, as I mentioned before, but as we’re in 2D, there’s no local dynamics associated with that part. But we’ll see in a moment that there’s very interesting stuff to take into account there too.) Anyway, the result for the Schwarzian dynamics can be written (see Stanford and Witten) in a way familiar from standard, say, statistical mechanics: $latex Z_0(\beta)=\int dE \rho_0(E) \exp(-\beta E)$, where $latex \rho_0(E)\sim\sinh(2\pi\sqrt{E})$ is the spectral density of the model. I now need to explain why everything has a subscript 0 in it in the last sentence.
  • On the other hand, the JT gravity model organises itself as a very interesting topological sum that is important if we are doing quantum gravity. First, recall that we’re working in the “Euclidean” manner discussed before (i.e., time is a spatial parameter, and so 2D space can be tessellated in that nice Escher way). The point is that the Einstein-Hilbert action in 2D is a topological counting parameter (as mentioned before, there’s no dynamics!). The thing that is being counted is the Euler characteristic of the space: $latex \chi=2-2g-b-c$, where $latex g,b,c$ are the number of handles, boundaries, and crosscaps the surface has, characterising its topology. Forget about crosscaps for now (that has to do with unorientable surfaces like a möbius strip $latex (g=0,b=1,c=1)$ – we’ll stick with orientable surfaces here). The full JT gravity action therefore has just the thing one needs to keep track of the dynamics of the quantum theory, and the partition function (or other quantities that you might wish to compute) can be written as a sum of contributions from every possible topology. So one can write the JT partition function as $latex Z(\beta)=\sum_{g=0}^\infty\hbar^{-(1-2g)}Z_g(\beta)$ where the parameter $latex \hbar$ weights different genus surfaces. In that sum the weight of a surface is $latex \hbar^{-\chi}$ and $latex b=1$ since there’s a boundary of length $latex \beta$, you may recall.

    The basic Schwarzian computation mentioned above therefore gives the leading piece of the partition function, i.e., $latex g=0$, and so that’s why I put the subscript 0 on it at the outset. A big question then is what is the result for JT gravity computed on all those other topologies?!

    • Click to continue reading this post →

Black Holes and a Return to 2D Gravity! – Part I

By | | , , , , ,
1 Comment

(A somewhat more technical post follows.) Well, I think I promised to say a bit more about what I’ve been up to in that work that resulted in the paper I talked about in an earlier post. The title of my paper, “Non-perturbative JT gravity” has JT (Jackiw-Teitelbiom) gravity in … Click to continue reading this post →

News from the Front XIX: A-Masing de Sitter

By | | , , , , ,
Comments Off on News from the Front XIX: A-Masing de Sitter

[caption id="attachment_19335" align="alignright" width="215"] Diamond maser. Image from Jonathan Breeze, Imperial College[/caption]This is part 2 of a chat about some recent thoughts and results I had about de Sitter black holes, reported in this arxiv preprint. Part 1 is here, so maybe best to read that first.

Now let us turn to de Sitter black holes. I mean here any black hole for which the asymptotic spacetime is de Sitter spacetime, which is to say it has positive cosmological constant. This is of course also interesting since one of the most natural (to some minds) possible explanations for the accelerating expansion of our universe is a cosmological constant, so maybe all black holes in our universe are de Sitter black holes in some sense. This is also interesting because you often read here about explorations of physics involving negative cosmological constant, so this is a big change!

One of the things people find puzzling about applying the standard black hole thermodynamics is that there are two places where the standard techniques tell you there should be a temperature associated with them. There’s the black hole horizon itself, and there’s also the cosmological horizon. These each have temperature, and they are not necessarily the same. For the Schwarzschild-de Sitter black hole, for example, (so, no spins or charges… just a mass with an horizon associated with it, like in flat space), the black hole’s temperature is always larger than that of the cosmological horizon. In fact, it runs from very large (where the black hole is small) all the way (as the black hole grows) to zero, where the two horizons coincide.

You might wonder, as many have, how to make sense of the two temperatures. This cannot, for a start, be an equilibrium thermodynamics system. Should there be dynamics where the two temperatures try to equalise? Is there heat flow from one horizon to another, perhaps? Maybe there’s some missing ingredient needed to make sense of this – do we have any right to be writing down temperatures (an equilibrium thermodynamics concept, really) when the system is not in equilibrium? (Actually, you could ask that about Schwarzschild in flat space – you compute the temperature and then discover that it depends upon the mass in such a way that the system wants to move to a different temperature. But I digress.)

The point of my recent work is that it is entirely within the realm of physics we have to hand to make sense of this. The simple system described in the previous post – the three level maser – has certain key interconnected features that seem relevant:

  • admits two distinct temperatures and
  • a maximum energy, and
  • a natural instability (population inversion) and a channel for doing work – the maser output.

My point is that these features are all present for de Sitter black holes too, starting with the two temperatures. But you won’t see the rest by staring at just the Schwarzschild case, you need to add rotation, or charge (or both). As we shall see, the ability to reduce angular momentum, or to reduce charge, will be the work channel. I’ll come back to the maximum […] Click to continue reading this post →

News from the Front, XVIII: de Sitter Black Holes and Continuous Heat Engines

By | | , , , ,
4 Comments

[caption id="attachment_19313" align="alignright" width="250"] Hubble photo of jupiter’s aurorae.[/caption]Another title for this could be “Making sense of de Sitter black hole thermodynamics”, I suppose. What I’m going to tell you about is either a direct correspondence or a series of remarkable inspiring coincidences. Either way, I think you will come away agreeing that there is certainly something interesting afoot.

It is an idea I’d been tossing around in my head from time to time over years, but somehow did not put it all together, and then something else I was working on years later, that was seemingly irrelevant, helped me complete the puzzle, resulting in my new paper, which (you guessed it) I’m excited about.

It all began when I was thinking about heat engines, for black holes in anti-de Sitter, which you may recall me talking about in posts here, here, and here, for example. Those are reciprocating heat engines, taking the system through a cycle that -through various stages- takes in heat, does work, and exhausts some heat, then repeats and repeats. And repeats.

I’ve told you the story about my realisation that there’s this whole literature on quantum heat engines that I’d not known about, that I did not even know of a thing called a quantum heat engine, and my wondering whether my black hole heat engines could have a regime where they could be considered quantum heat engines, maybe enabling them to be useful tools in that arena…(resulting in the paper I described here)… and my delight in combining 18th Century physics with 21st Century physics in this interesting way.

All that began back in 2017. One thing I kept coming back to that really struck me as lovely is what can be regarded as the prototype quantum heat engine. It was recognized as such as far back as 1959!! It is a continuous heat engine, meaning that it does its heat intake and work and heat output all at the same time, as a continuous flow. It is, in fact a familiar system – the three-level maser! (a basic laser also uses the key elements).

A maser can be described as taking in energy as heat from an external source, and giving out energy in the form of heat and work. The work is the desired […] Click to continue reading this post →