Black Holes and a Return to 2D Gravity! – Part II
(A somewhat more technical post follows.)
Continuing from part I: Well, I set the scene there, and so after that, a number of different ideas come together nicely. Let me list them:
[caption id="attachment_19442" align="alignright" width="250"]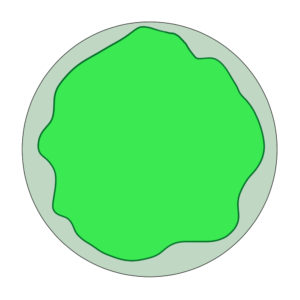
What “nearly” AdS_2 looks like via JT gravity. The boundary wiggles, but has fixed length 1/T.[/caption]
- Exact solution of the SYK model (or dual JT model) in that low temperature limit I mentioned before gave an answer for the partition function $latex Z(\beta)$, by solving the Schwarzian dynamics for the wiggling boundary that I mentioned earlier. (The interior has a model of gravity on $latex AdS_2$, as I mentioned before, but as we’re in 2D, there’s no local dynamics associated with that part. But we’ll see in a moment that there’s very interesting stuff to take into account there too.) Anyway, the result for the Schwarzian dynamics can be written (see Stanford and Witten) in a way familiar from standard, say, statistical mechanics: $latex Z_0(\beta)=\int dE \rho_0(E) \exp(-\beta E)$, where $latex \rho_0(E)\sim\sinh(2\pi\sqrt{E})$ is the spectral density of the model. I now need to explain why everything has a subscript 0 in it in the last sentence.
- On the other hand, the JT gravity model organises itself as a very interesting topological sum that is important if we are doing quantum gravity. First, recall that we’re working in the “Euclidean” manner discussed before (i.e., time is a spatial parameter, and so 2D space can be tessellated in that nice Escher way). The point is that the Einstein-Hilbert action in 2D is a topological counting parameter (as mentioned before, there’s no dynamics!). The thing that is being counted is the Euler characteristic of the space: $latex \chi=2-2g-b-c$, where $latex g,b,c$ are the number of handles, boundaries, and crosscaps the surface has, characterising its topology. Forget about crosscaps for now (that has to do with unorientable surfaces like a möbius strip $latex (g=0,b=1,c=1)$ – we’ll stick with orientable surfaces here). The full JT gravity action therefore has just the thing one needs to keep track of the dynamics of the quantum theory, and the partition function (or other quantities that you might wish to compute) can be written as a sum of contributions from every possible topology. So one can write the JT partition function as $latex Z(\beta)=\sum_{g=0}^\infty\hbar^{-(1-2g)}Z_g(\beta)$ where the parameter $latex \hbar$ weights different genus surfaces. In that sum the weight of a surface is $latex \hbar^{-\chi}$ and $latex b=1$ since there’s a boundary of length $latex \beta$, you may recall.
The basic Schwarzian computation mentioned above therefore gives the leading piece of the partition function, i.e., $latex g=0$, and so that’s why I put the subscript 0 on it at the outset. A big question then is what is the result for JT gravity computed on all those other topologies?!
Back where? In front of a classroom teaching quantum field theory, that is. It is a wonderful, fascinating, and super-important subject, and it has been a while since I’ve taught it. I actually managed to dig out some pretty good notes for the last time I taught it. (Thank you, my inner pack rat for keeping those notes and putting them where I could find them!) They’ll be a helpful foundation. (Aren’t they beautiful by the way? Those squiggly diagrams are called Feynman diagrams.)
