 It was a fun week in the string theory class this week, as we got to some major landmarks that are always fun to teach. We’ve uncovered the extended objects called D-branes (see numerous previous posts for how useful and important these objects are in string theory research) in all their glory in the lectures before, and deduced lots of their properties, such as the form of the action that determines how a D-brane moving in spacetime responds to the various fields (including the geometry) created by the string theory. That’s all fun, but then the key thing to do next is to compute the mass of these dynamical objects, or the mass per unit volume – the tension. Computing it fully, with no hand-wavy factors. Your mass measures how strongly you interact with gravity. So you can measure it by studying the gravitational interaction between masses. (You do that when you step on a scale to measure your weight… well the scale does it by showing how much force it takes to stop you from falling through the floor toward the center of the earth…)
It was a fun week in the string theory class this week, as we got to some major landmarks that are always fun to teach. We’ve uncovered the extended objects called D-branes (see numerous previous posts for how useful and important these objects are in string theory research) in all their glory in the lectures before, and deduced lots of their properties, such as the form of the action that determines how a D-brane moving in spacetime responds to the various fields (including the geometry) created by the string theory. That’s all fun, but then the key thing to do next is to compute the mass of these dynamical objects, or the mass per unit volume – the tension. Computing it fully, with no hand-wavy factors. Your mass measures how strongly you interact with gravity. So you can measure it by studying the gravitational interaction between masses. (You do that when you step on a scale to measure your weight… well the scale does it by showing how much force it takes to stop you from falling through the floor toward the center of the earth…)
 So in class this is when we go all Polchinski and unpack the tension computation, stopping to admire the various features of string theory you learn along the way, and seeing how simply beautifully the various basic features of the superstring theories that we’ve met in the last few lectures encode themselves in one nice object – the vacuum amplitude [tex] {\cal A }[/tex] from the cylinder diagram representing either exchange of closed strings (including quanta like the graviton – this is what you focus on to learn what the mass is) between a pair of D-branes, or an open string with its ends tethered to a pair of D-branes going in a closed loop. That there are two ways of looking at the diagram, an open string way (running time around the cylinder) and a closed string way (running time along the cylinder) is a hugely powerful thing, and is at the heart of so very much of what we do in string theory these days especially – including a lot of what I’ve told you in previous posts (see e.g. here and here) about applications to things of interest in current experiments.
So in class this is when we go all Polchinski and unpack the tension computation, stopping to admire the various features of string theory you learn along the way, and seeing how simply beautifully the various basic features of the superstring theories that we’ve met in the last few lectures encode themselves in one nice object – the vacuum amplitude [tex] {\cal A }[/tex] from the cylinder diagram representing either exchange of closed strings (including quanta like the graviton – this is what you focus on to learn what the mass is) between a pair of D-branes, or an open string with its ends tethered to a pair of D-branes going in a closed loop. That there are two ways of looking at the diagram, an open string way (running time around the cylinder) and a closed string way (running time along the cylinder) is a hugely powerful thing, and is at the heart of so very much of what we do in string theory these days especially – including a lot of what I’ve told you in previous posts (see e.g. here and here) about applications to things of interest in current experiments.
One of the fun things about all this is that the answer is actually [tex]{\cal A}=0[/tex]. It is zero because all the infinite modes of oscillation of the string gather themselves up nicely to give a factor:
[tex]
q^{-\frac{1}{6}}\prod_{n=1}^{\infty}(1+q^{n-\frac{1}{2}})^8-q^{-\frac{1}{6}}\prod_{n=1}^{\infty}(1-q^{n-\frac{1}{2}})^8-16q^{\frac{1}{3}}\prod_{n=1}^{\infty}(1+q^{n})^8=0\ .
[/tex]
Think of [tex]q[/tex] as a book-keeping device that lets one track energy contributions (in the power of it that appears in a term if one expanded this expression), and how many […] Click to continue reading this post →
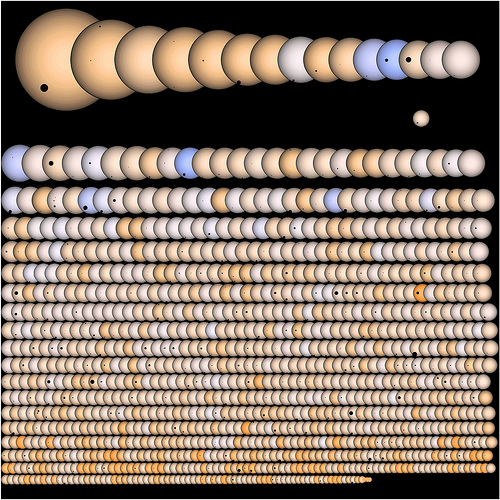 The exo-planet hunting craft Kepler has found 1235 candidate planets orbiting other suns so far. The APOD site has a lovely composition by Jason Rowe showing representations of all of those suns with the spots on them that represent the planet transiting in front of them (that’s how they are found by Kepler). They are all nicely […] Click to continue reading this post
The exo-planet hunting craft Kepler has found 1235 candidate planets orbiting other suns so far. The APOD site has a lovely composition by Jason Rowe showing representations of all of those suns with the spots on them that represent the planet transiting in front of them (that’s how they are found by Kepler). They are all nicely […] Click to continue reading this post 








 It was a fun week in the string theory class this week, as we got to some major landmarks that are always fun to teach. We’ve uncovered the extended objects called D-branes (see numerous previous posts for how useful and important these objects are in string theory research) in all their glory in the lectures before, and deduced lots of their properties, such as the form of the action that determines how a D-brane moving in spacetime responds to the various fields (including the geometry) created by the string theory. That’s all fun, but then the key thing to do next is to compute the mass of these dynamical objects, or the mass per unit volume – the tension. Computing it fully, with no hand-wavy factors. Your mass measures how strongly you interact with gravity. So you can measure it by studying the gravitational interaction between masses. (You do that when you step on a scale to measure your weight… well the scale does it by showing how much force it takes to stop you from falling through the floor toward the center of the earth…)
It was a fun week in the string theory class this week, as we got to some major landmarks that are always fun to teach. We’ve uncovered the extended objects called D-branes (see numerous previous posts for how useful and important these objects are in string theory research) in all their glory in the lectures before, and deduced lots of their properties, such as the form of the action that determines how a D-brane moving in spacetime responds to the various fields (including the geometry) created by the string theory. That’s all fun, but then the key thing to do next is to compute the mass of these dynamical objects, or the mass per unit volume – the tension. Computing it fully, with no hand-wavy factors. Your mass measures how strongly you interact with gravity. So you can measure it by studying the gravitational interaction between masses. (You do that when you step on a scale to measure your weight… well the scale does it by showing how much force it takes to stop you from falling through the floor toward the center of the earth…) 



