In class tomorrow I’ll introduce one of my favourite equations:
[tex]
\frac{d^2x^\sigma}{d\tau^2}+\Gamma^\sigma_{\rho\nu}\frac{dx^\rho}{d\tau}\frac{dx^\nu}{d\tau}= 0\ .
[/tex]
… Wait – Where did everyone go?!
Come back! I’m not expecting you to know what it means, I just wanted to talk a bit with it sort of … nearby. If you consider yourself a bit intimidated by mathematics, be assured that it won’t bite. (No more than a piece of sheet music lying nearby will harm someone who has not learned to read music.)
It turns out that it is pretty geometry! In the equation, we’ve the object
[tex]
\Gamma^{\sigma}_{\rho\nu}\equiv\frac12 g^{\sigma\mu}\Biggl(\frac{\partial g_{\mu\nu}}{\partial x^\rho}+\frac{\partial g_{\mu\rho}}{\partial x^\nu}-\frac{\partial g_{\rho\nu}}{\partial x^\mu}\Biggr)\ ,
[/tex]
called the “Christoffel symbols”. The set of objects [tex]g_{\mu\nu}[/tex] (the “metric”) actually encode the properties of the space you wish to study (like the plane, or the sphere), and the equation at the top tells you what are the “straight lines” in that space. Well, in the plane (like your desktop) they are straight lines, while in other spaces they are the analogue of straight lines – if you want to go from one point to another point somewhere else in the space and desire to travel along the shortest path to do so, you want to follow such a line. It is called a “geodesic”. The equation is commonly called the geodesic equation.
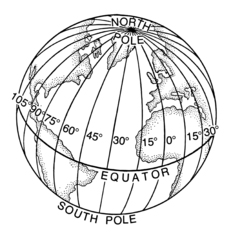 You know such lines, intuitively, in a non-trivial example. Next time you look at a globe (wait, does anyone but me look at maps and globes any more? I love them!), you’ll probably see examples of those lines drawn in. They are the “great circles”, the lines of longitude, and the equator. (Image used with permission.)
You know such lines, intuitively, in a non-trivial example. Next time you look at a globe (wait, does anyone but me look at maps and globes any more? I love them!), you’ll probably see examples of those lines drawn in. They are the “great circles”, the lines of longitude, and the equator. (Image used with permission.)
I just made a class worksheet that guides one through a bit of playing with this equation to get the class excited about […] Click to continue reading this post →

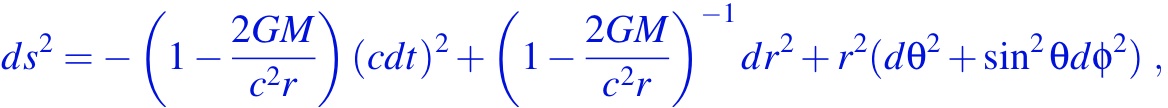

 You know such lines, intuitively, in a non-trivial example. Next time you look at a globe (wait, does anyone but me look at maps and globes any more? I love them!), you’ll probably see examples of those lines drawn in. They are the “great circles”, the lines of longitude, and the equator. (Image used with
You know such lines, intuitively, in a non-trivial example. Next time you look at a globe (wait, does anyone but me look at maps and globes any more? I love them!), you’ll probably see examples of those lines drawn in. They are the “great circles”, the lines of longitude, and the equator. (Image used with 






















