(A more technical post follows.)
By the way, in both sets of talks that I mentioned in the previous post, early on I started talking about orthogonal polynomials  , and how they generically satisfy a three-term recurrence relation (or recursion relation):
, and how they generically satisfy a three-term recurrence relation (or recursion relation):

Someone raised their hand and ask why it truncates to three terms and on the spot I said that I’d forgotten the detailed proof (it has been many years since I thought about it) but recall that it follows straightforwardly from orthogonality. Lack of time meant that I did not want to try to reconstruct the proof on the board in real time, but it is a standard thing that we all use a lot because it is true for all the commonly used families of polynomials in lots of physics, whether it be Hermite, Legendre, Laguerre, Chebyshev, etc. Anyway, I finally got around to reminding myself of it and thought I’d record it here. Now all I have to do in future is point people here as a handy place to look it up. ([Although you can find equivalent discussions in several sources, for example this nice YouTube lecture here, which is part of a lovely series of lectures on polynomial approximation of functions, which is a fascinating topic in its own right.]
Ok, I should quickly remind what the setup is. The polynomials are normalised so that the  th one is
th one is  (they’re “monic”) and they are orthogonal with respect to the measure
(they’re “monic”) and they are orthogonal with respect to the measure  where
where  is called the “weight function” (it has some suitable properties we won’t worry about here). In the case of random matrix models we have
is called the “weight function” (it has some suitable properties we won’t worry about here). In the case of random matrix models we have  for some potential
for some potential  (here
(here 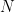 is the size of the matrix; in this problem it is just a normalisation choice – you can just as well absorb it into the potential).
is the size of the matrix; in this problem it is just a normalisation choice – you can just as well absorb it into the potential).
So we have the inner product:

defining the orthogonality, where the 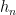 are some positive non-vanishing normalisation constants. Ok now we are ready for the proof.
are some positive non-vanishing normalisation constants. Ok now we are ready for the proof.
Imagine there are terms in the recursion beyond the three terms. Let’s write these “remainder” terms as a linear combination of all lower polynomials up to degree n-2, so the recursion is tentatively:
 .
.
Taking the inner product  for
for  or
or 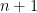 just tells you the definition of the recursion coefficients
just tells you the definition of the recursion coefficients 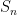 and
and  in terms of ratios of inner products for those
in terms of ratios of inner products for those  , and for
, and for  any higher you get zero since the polynomial is then of too high order to give anything non-zero.
any higher you get zero since the polynomial is then of too high order to give anything non-zero.
So  and
and  .
.
Then you take the inner product  for the cases m < n-2.
for the cases m < n-2.
But this is also (by definition; I can let the lambda act in the opposite direction inside the integral)  , which vanishes since the degree of the first entry,
, which vanishes since the degree of the first entry, 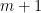 , is less than
, is less than  , and so it can only contain polynomials of degree less than
, and so it can only contain polynomials of degree less than  which are orthogonal to
which are orthogonal to  . Therefore the inner product says
. Therefore the inner product says  in all those cases, which means that
in all those cases, which means that  for
for  .
.
That’s it. All done. Except for the remark that given the expression for 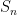 above, when the weight function is even, the
above, when the weight function is even, the 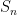 vanish. (This is the case for even potentials in the case of random matrix models.)
vanish. (This is the case for even potentials in the case of random matrix models.)
Ok, one more useful thing: It is clear from the definition of the inner product integral that  . But you can also write this as
. But you can also write this as  and use the recursion relation
and use the recursion relation  , and all these terms vanish in the integral except the last, and so we get
, and all these terms vanish in the integral except the last, and so we get  .
.
Hence we’re derived an important relation: 
(We essentially got this already in the earlier equation for  ; just rearrange the action of
; just rearrange the action of 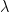 up there again.)
up there again.)
–cvj
 Never toured the inside of the Houses of Parliament before, seeing all the red and green colour coded areas (lords and commons – look at the benches next time you see debates in either place) and busts and statues of some of the shapers, for better or worse, of much of the fabric of UK democracy. (Thanks to my sister for this wonderful opportunity on Friday!) BTW, most of the interesting stuff I saw was off limits to photos, sorry!
Never toured the inside of the Houses of Parliament before, seeing all the red and green colour coded areas (lords and commons – look at the benches next time you see debates in either place) and busts and statues of some of the shapers, for better or worse, of much of the fabric of UK democracy. (Thanks to my sister for this wonderful opportunity on Friday!) BTW, most of the interesting stuff I saw was off limits to photos, sorry!













