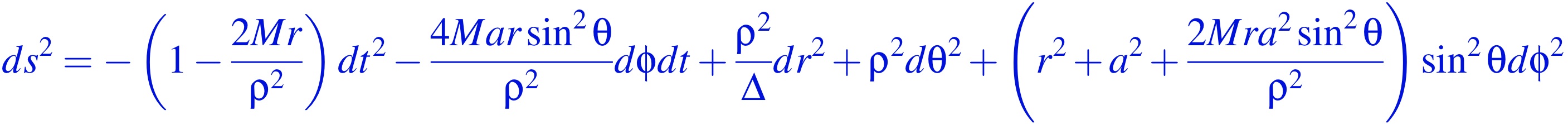Bigger than the FCC
We’ve been studying rotating black holes in my class this week, which has been fun. We get to apply the techniques we’ve been honing in the context of the Schwarzschild solution (link to recent posts below) to a bit more complicated solution, the Kerr solution, which includes rotation. Some equations follow, although you needn’t be put off by them. Most of this will make sense without really understanding them much. Just so you can see the shape of the things we scribble, I’ll show you the equation that captures this curved spacetime geometry, with no real explanation (sorry):
Here [tex]\Delta\equiv r^2-2Mr+a^2[/tex] and [tex]\rho^2\equiv r^2+a^2\cos^2\theta\ .[/tex] The parameter [tex]a[/tex] is the ratio of the solution’s spin or angular momentum [tex]J[/tex] to its total mass [tex]M[/tex], measured in appropriate units. It’s a very important solution to get to grips with, since it’s not just fantasy physics, but highly relevant for astrophysics since black holes that are “out there” are unlikely to be non-rotating, and in fact, one can expect them to be rotating at quite a clip in many cases. A good many black holes – including some of the […] Click to continue reading this post