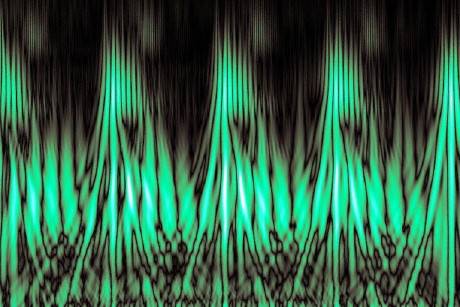
What is this? It’s whale song, obviously! Not so obvious? Ok, let’s take a step back. You’ve heard whale song, no doubt. Either in the context of movies, a cheesy movement a decade ago of adding clips of them to pop and rock songs, wildlife documentaries, and so forth. It’s lovely and mysterious, and -new age poppycock aside- really quite captivating. There are a lot of scientific questions about whale song too. Are these noises random? Is there content? How much content? How individual-whale-specific is a whale song? If there’s information, is it wisdom of the ancients, directiions to food, or just gossip about whale celebrities?
All questions you’ve asked yourself too, I don’t doubt.
Well, some of our best minds are on the job, you’ll be pleased to know. One of them, Mark Fischer, is taking a new approach to the problem, with rather beautiful results. He is using a wavelet transform (Amara’s wavelet site, and a wikipedia link, both giving information about what that is) to analyze whale songs and then colour coding them (among other things) to aid in visualizing the results. The results are quite striking, I hope you agree, and here’s another:

There’s a New York Times article on his work that can be found here, and from which I quote:
Mr. Fischer creates visual art from sound using wavelets. Once relatively obscure, wavelets are being used in applications as diverse as JPEG image compression, high definition television and earthquake research, said Gilbert Strang, a math professor at the Massachusetts Institute of Technology and an expert on wavelets.
They are popular now in part because they can capture intricate detail without losing the bigger picture, and when presented in circular form (using a cylindrical coordinate system [click on image at right -cvj]), repeated patterns are even more evident. By stringing successive images together, Mr. Fischer transforms still images into animated audio files that bring the sound to life.
Fischer is very keen to stress both the scientific and artist value of these representations. His web site is at this link. Scientists working in these areas using more “traditional” methods may well adopt this or similar methods as a tool. Here’s a quote from the article from one of them. For example:
Peter Tyack agrees that the technique has potential not only as art, but as a scientific research tool. A senior scientist at Woods Hole Oceanographic Institution, Dr. Tyack studies the way humpback whales communicate, trying to show that the repetitions in whale songs follow grammatical rules similar to those of human language.
“Looking at those figures, it looked like you could see a lot of repeated units,†Dr. Tyack said of the images. “It looks like he’s visualizing some of the points that we made in the paper about humpback song.â€
Earlier today Amara Graps, a regular and informative commenter here and on CV told me more about this, and gave me some nice links that she said I can share with you. First, as I pointed out earlier, there’s her website on wavelets in general.
She says:
He transforms whale calls using wavelet transforms, and more
recently turned those gorgeous pictures into animations playing
simultaneously with the calls. Here are his animations on Google Video: (link).My favorite is this (part of the the Nollman session described
below minus the guitar)
If you go to Amara’s Wavelet Sound Fun page (and who would not want to with a title like that), you’ll learn a bit more about other applications of wavelet transforms, and you can scroll down to the bit on whale song to see more description of Mark’s work.
Enjoy!
-cvj


Interesting idea…!
-cvj
Hi. I think it would be pretty nifty to see this done with “earthsongs”, the geomagnetic recordings from space. Check it out on spaceweather or just Google it, I am sure you will find it. I love the image presentation and the dynamics given to the whale song here. I only suggest this because I would love to see the comparitive with such depth. Thank you!
Hi,
I’m not following. Precisely what similarities do you have in mind, exactly?
-cvj
I might like to add that if the AdS/CFT correspondence is indeed a sort of wavelet transform, it would have to be a nonlinear wavelet transform, which is a bit atypical.
Is it just me, or has anyone else noticed the similarities between wavelet transforms and the AdS/CFT correspondence holography? Maybe the latter is an example of the former?
People that I’ve mentioned this observation to in the past don’t seem to take this idea seriously.
Hi Amara- it is so nice to hear from you. See what happens when you write ‘wavelets for beginners’??
There is one small typo in the NY Times article. The mandalas are wavelet transforms presented in polar (of course), not cylindrical.
The movies are colored using normalized power spectral density functions, mapped over the conventional ROYGBIV (rainbow spread) from low frequencies to the highest. But they are -normalized-, so a particular color can map to quite different frequencies from movie to movie. And what is up on Google Video is positively grainy compared to the originals. Doesn’t seem to be any way around that, at the moment. 🙁
Stills, on the other hand, are fair game for artistic license.
Whales do some amazing things with sound. The Beluga sphere, for example. Or the ‘max co’ graph of a Blue whale song described in:
http://aguasonic.com/Cetacean/Fifty2
Or, one of the most mysterious- the Pilot’s Chorus.
There are indications that at least some of these sounds have nothing to do with ‘communication’ as we would understand it. More like ‘communion’.
I am working on animating the polar form- stay tuned.
Namaste,
Mark
~~~~
thank you.
woops, I gave a wrong link (still asleep): my main wavelet site (Clifford mentioned too) is here.
A cornellian: The two large rectangular images show a time-frequency plane with time on the x axis and frequency on the y axis. Every 1D time series would be split into this type of of 2D representation with a wavelet transform, but there are a variety of different wavelet transforms. I think the above were transformed with a continuous wavelet transform, which means that the data was over-sampled in both time and frequency. Wavelet transforms use a mathematical function ‘wavelet’ which is limited in length and which satisfy certain basis function criteria, and there are many of these functions to choose from, depending on what you want to do. Once you have chosen your wavelet, then your wavelet transform consists of you projecting that wavelet over your data, again and again, each time stretching or shrinking the wavelet and displacing it in time, in order to pick out different parts of your time series. In the places where the wavelet matches the time series, the coefficients will be large, where it doesn’t, the coefficient values will small. Mark chose different color tables corresponding to the coefficient values so the brightest represent the high valued coefficients. Because you are using different sizes of the wavelet, and shifted in time, then the small versions of the wavelet will return to you the high frequency components of your time series, while the large versions of the wavelet wil return to you the low frequency components. It looks like the two images are oriented so that they have the lower frequency components at the bottom end of the y-axis and the higher frequency components are along the top.
For anyone not familiar with wavelets, my wavelet site is a good site for beginners to learn about wavelets. It emerged 11 years ago from me being a beginner. (Now I’m an advanced beginner!) I’ve never been a wavelet researcher, but I’ve written alot of wavelet code and I have applied wavelets to a lot of time series data. At my wavelet site you’ll find a relatively non-mathematical Introduction to wavelets article that I wrote in 1995, along with links to many other people’s wavelet perspectives, so happy browsing.
And if anyone here knows if wavelets have ever been applied to analyzing Cremona violins (Stradivarius, Guarnieris), see here under “Violins”, please drop me an email, I am still keen to know.
These are all well and pretty, but what are the axes and what do the colors mean?